CVSim as a learning tool. II Interfacial concentrations

Cyclic voltammetry and interfacial concentrations of electroactive species

Let us consider a reversible, or Nernstian, redox reaction (E) A + e $\leftrightarrow$ B assuming semi-infinite linear diffusion and a solution initially containing only species A ($C_\mathrm B^*=0$), studied by cyclic voltammetry. The change of the concentrations of species A and B with electrode potential is shown in Fig. 1. It is tempting to explain qualitatively the shape of the voltammogram by saying that the interfacial concentration in A decreases and becomes zero at the peak potential, where the current is maximum in absolute value.

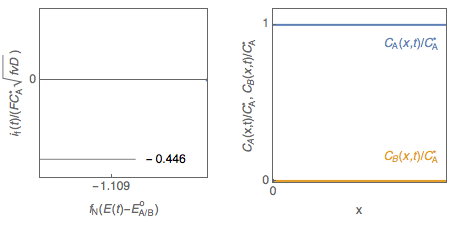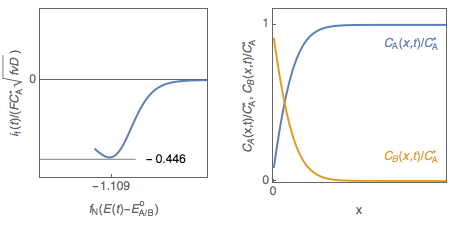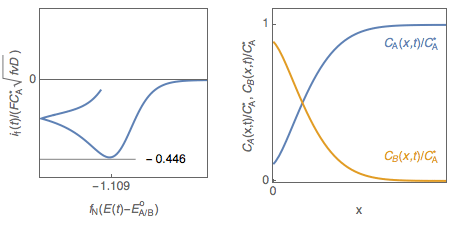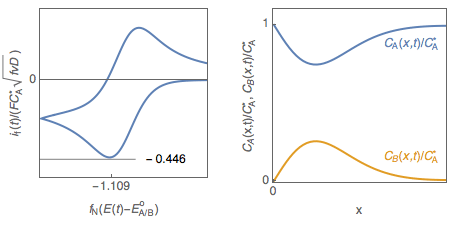
Figure 1: Cyclic voltammetry for reversible redox reaction and change of the concentration profiles of species A and B with electrode potential. 

However, the interfacial concentration $C_\mathrm A(0,t)$ is not close to zero at the peak potential as shown in Fig. 2, plotted using CVSim.

Interfacial concentration of A at the current peak

The potential for which the current reaches an extremum, also named peak potential $E_{\mathrm{p}}$ is given for equal diffusion coefficients of the two species A and B by [1,2]

$$ E_{\mathrm{p}}=E^\mathrm o_\text{A/B} -\frac{1,109}{f_\mathrm N} \Rightarrow f_\mathrm N(E_{\mathrm{p}}-E^\mathrm o_\text{A/B})=-1,109,\;f_\mathrm N=F/(R\,T) \tag 1$$

For a Nernstian redox reaction the interfacial concentrations $C_\mathrm A(0,t)$ and $C_\mathrm B(0,t)$ of species A and B follow Nernst’s law outside equilibrium

$$ E(t)=E^\mathrm o_\text{A/B}+\frac{1}{f_\mathrm N}\,\ln \frac{C_\mathrm A(0,t)}{C_\mathrm B(0,t)}\Rightarrow f_\mathrm N(E(t)-E^\mathrm o_\text{A/B})=\ln \frac{C_\mathrm A(0,t)}{C_\mathrm B(0,t)} \tag 2$$ and, for the peak potential $t=t_\mathrm{p}$

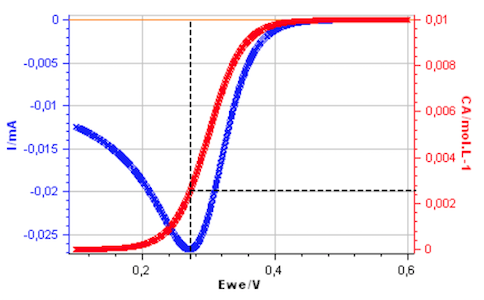
Figure 2: Cyclic voltammetry for a reversible redox reaction and change of $C_\mathrm A(0,t)$ with electrode potential.

Interfacial concentration of A at the current peak

The potential for which the current reaches an extremum, also named peak potential $E_{\mathrm{p}}$ is given for equal diffusion coefficients of the two species A and B by [1,2]

$$ E_{\mathrm{p}}=E^\mathrm o_\text{A/B} -\frac{1,109}{f_\mathrm N} \Rightarrow f_\mathrm N(E_{\mathrm{p}}-E^\mathrm o_\text{A/B})=-1,109,\;f_\mathrm N=F/(R\,T) \tag 1$$

For a Nernstian redox reaction the interfacial concentrations $C_\mathrm A(0,t)$ and $C_\mathrm B(0,t)$ of species A and B follow Nernst’s law outside equilibrium

$$ E(t)=E^\mathrm o_\text{A/B}+\frac{1}{f_\mathrm N}\,\ln \frac{C_\mathrm A(0,t)}{C_\mathrm B(0,t)}\Rightarrow f_\mathrm N(E(t)-E^\mathrm o_\text{A/B})=\ln \frac{C_\mathrm A(0,t)}{C_\mathrm B(0,t)} \tag 2$$

and, for the peak potential $t=t_\mathrm{p}$

$$\frac{C_\mathrm A(0,t_{\mathrm{p}})}{ C_\mathrm B(0,t_{\mathrm{p}})}=\exp(-1,109) \tag 3 $$

Writing, as in the steady state conditions, that the concentrations $C_\mathrm A(0,t)$ and $C_\mathrm B(0,t)$ are related, for equal diffusion coefficients of the two species A and B, by the relationship

$$C_\mathrm A(0,t_{\mathrm{p}})+C_\mathrm B(0,t_{\mathrm{p}})=C_\mathrm A^* \tag 4$$

since $C_\mathrm B^*=0$.

Using the Eqs.~(3) et (4), we have:

$$\frac{C_\mathrm A(0,t_{\mathrm{p}})}{C_\mathrm A^*}=  24.8\;\% \tag 5$$

The interfacial concentration of A, for a Nernstian redox reaction, is therefore not close to zero at the peak potential of the voltammogram in agreement with Fig. 2.

[1] A. J. Bard and L. R. Faulkner. Electrochemical methods. Fundamentals and Applications. John Willey & Sons, New York, 1980.

[2] J.-P. Diard, B. Le Gorrec, and C. Montella. Cinétique electrochimique. Hermann, Paris, 1996.