QCM: Why measure at overtones matters

Check out our partners to perform coupled measurements: https://www.biologic.net/partners

As previously mentioned [1], common QCM systems measure the fundamental resonant frequency changes and sometimes the resistance, which can somehow be related to the dissipative properties of the film or medium.

Advanced systems based on impedance or ring down measurements give access to the true dissipation or half bandwidth or quality factor and allow measurements at several overtones[1]. The number of allowed overtones depends on the bandwidth of the instrument and on the fundamental resonant frequency of the quartz.

The overtone order must be odd (1, 3, 5…) to ensure an antisymmetric pattern of motion of the quartz. If the overtone order is even (2, 4, 6…) the deformation is symmetric and there is no current between the electrodes [4].

Figure 1 shows the vibrational movement of quartz at the fundamental frequency $f_0$ (Top) and the third harmonic $3f_0$ (Bottom).

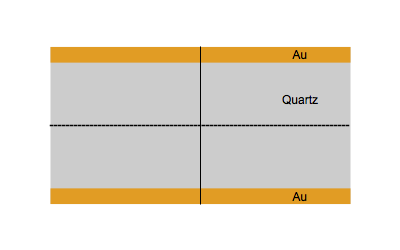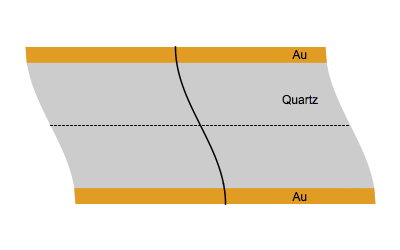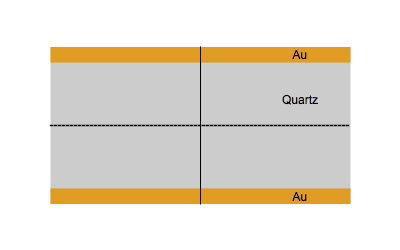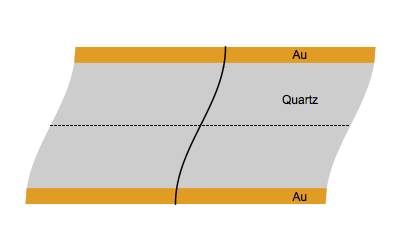
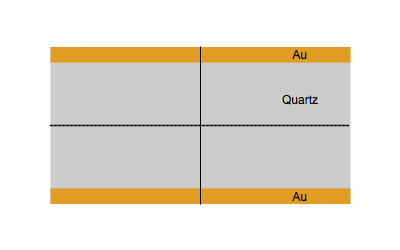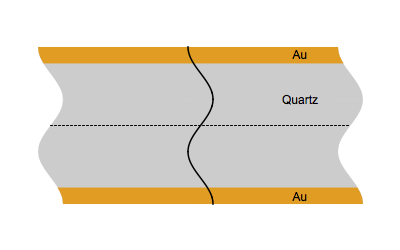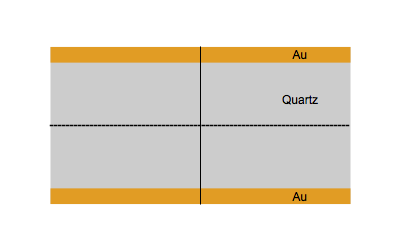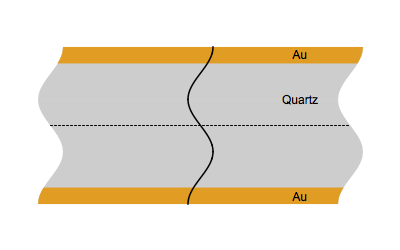
Figure 1: Quartz at the fundamental frequency $f_0$ (Top) and the third harmonic $3f_0$ (Bottom).

Why measure overtones or harmonics? Ensuring the validity of the Sauerbrey equation.

Measuring at harmonics gives another way of ensuring that the film coating the bare electrode is rigid. If the value $\Delta f_n/n$  is constant for each harmonic, the film can be considered rigid.

Measurements at overtones are more reliable

The value $\Delta f_n/n$, where $f_n$ is the resonant frequency at the $n^{th}$ harmonic, should theoretically be constant with the harmonic order. However, it has been noted [3] that it was constant only after the $3^{\text{rd}}$ harmonic, which then can be considered to be a more reliable measurement of the resonant frequency change. This can be seen in Fig.2 taken from [5].

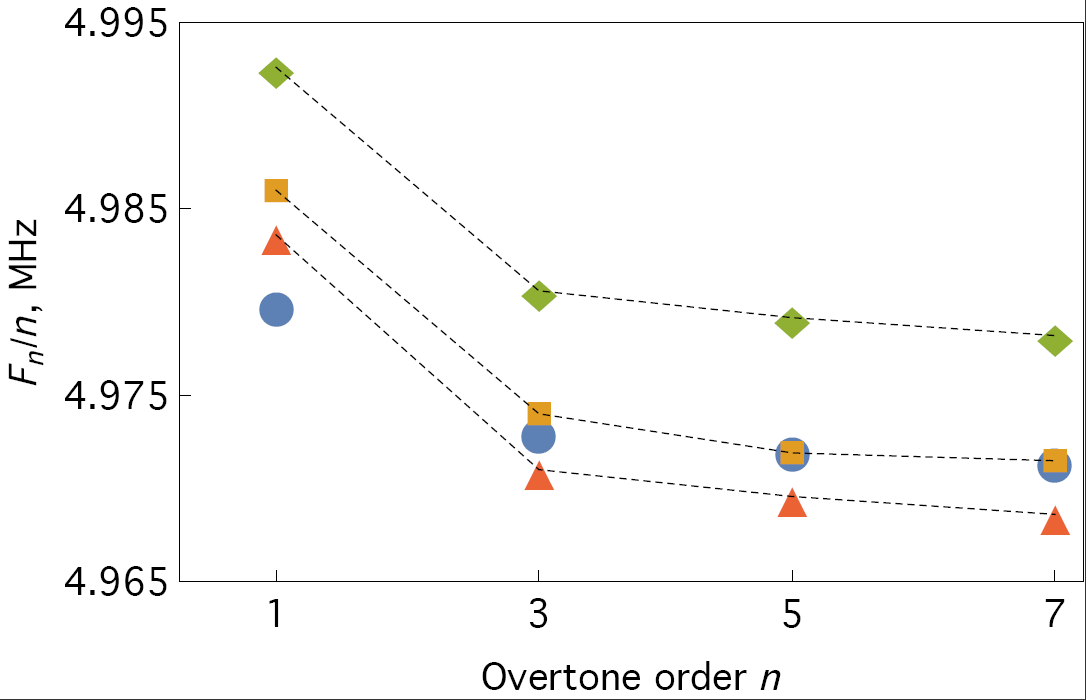
Figure 2: The absolute frequency of several 5 MHz crystals–#60, 66, and 67 (two measurements): (solid shapes) measured on various overtones with a QCM-D instrument in air, compared with the values of (open shapes) $f_n/n$ obtained theoretically. All frequencies are scaled by the overtone order.

Measurements at harmonics are needed for advanced data interpretation

Dissipation and resonant frequency shift are needed at several harmonics when one needs to study and characterize visco-elastic homogeneous thin films, particles, molecules, or conformation.

As long as the studied object is the growth or deposition of a rigid thin film or Sauerbrey thin film or elastic film, the mechanical response does not depend on the frequency. This is not the case when the object of study is a visco-elastic film, that is to say, a film where the energy of the wave is both elastically transferred and viscously dissipated. In this case, the response of the system composed of the quartz, the electrodes, the film, and the medium (air or liquid) depends on the input frequency.

A parallel can be made between the electrical transfer function of a system, for example, the impedance, and the mechanical transfer function of a system, for example, the shear modulus. In the same manner that the impedance $Z(\omega)$ (with $\omega=2\pi f$) allows the calculation of the current response from the potential input, the shear modulus $G(\omega)$ allows the calculation of the stress response from the strain input. In a visco-elastic film, the shear modulus is a frequency-dependent complex function.

$G(\omega)=\mathrm{Re}(G(\mathrm{\omega}))+j\;\mathrm{Im}(G(\mathrm {\omega}))$

More details can be found in [4].

[1] Quartz Crystal Microbalance: Measurement principles

[2] https://en.wikipedia.org/wiki/Overtone

[3] https://en.wikipedia.org/wiki/Harmonic

[4] D. Johannsmann, in “The quartz crystal microbalance in soft matter research”, Springer, 2015

[5] I. Reviakine, A. N. Morozov, F. F. Rossetti, J. Appl. Phys. 95 (2004) 7712.

1. Overtones and harmonics are similar terms although it seems that overtones are mainly used in the field of acoustics. Furthermore, whereas “harmonics” mean multiple integers of the fundamental frequency, including the fundamental frequency, “overtones” seem to mean any multiple of and over the fundamental frequency, excluding the fundamental frequency [2,3].