Topic 10 min read

Koutecký-Levich analysis: the principles

Latest updated: November 18, 2024

The Koutecký-Levich analysis allows researchers to simply and quickly obtain critical kinetic parameters for a redox reaction such as the standard reaction constant k° and the symmetry factor α.

The raw data on which this analysis is performed are the same as the data on which the Levich analysis is performed [1,2] that is to say steady-state I vs. E curves at various rotation rates of the disk electrode.

Determination of k° and α

First and foremost, it should be noted that in theory, the Koutecký-Levich analysis only works for redox reactions with a standard kinetic constant k° smaller or equal to several 10^-2 cm s^-1, that is to say, for sluggish reactions. In practice, most reactions are neither sluggish nor rapid. The first step is to plot at a fixed potential the values of the current at the various rotation rates (Fig. 1a). The value of the potential is chosen before the current plateau.

The second step is to plot the inverse of the current values as a function of the inverse of the square root of the rotation speed (Fig. 1b). This is what is called the Koutecký-Levich plot.

The third step is to extrapolate the Koutecký-Levich line to 0, which corresponds to a theoretical infinite rotation speed (Fig. 1c, black dot). At this point, the current value corresponds to the electronic transfer current i_t, that is to say, the current that you would obtain if there was absolutely no limitation by mass transport (ie Tafelian, Butler-Volmer, Stern or Wagner-Traud kinetics).

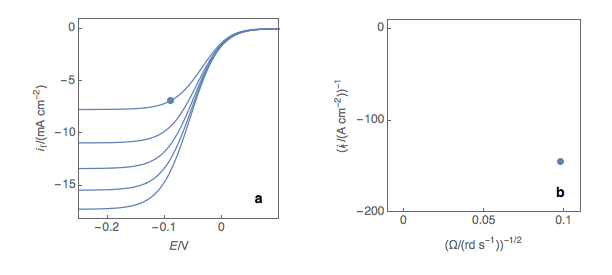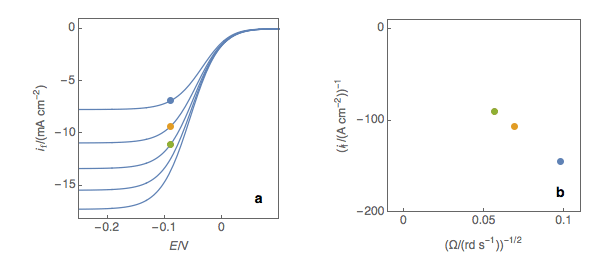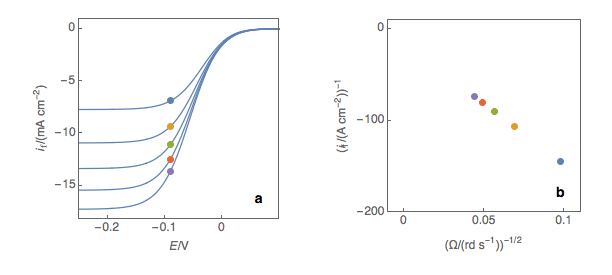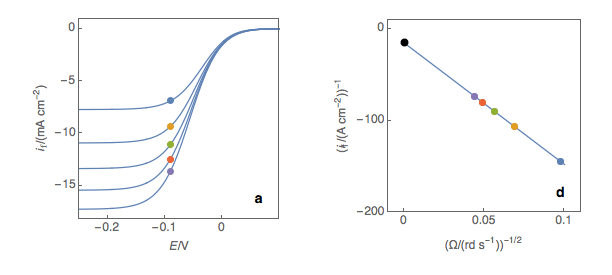
Figure 1: (a) I vs. E curves obtained on an irreversible system on a Rotating Disk Electrode at
various rotation speeds. The dots represent the points chosen to plot the Koutecký-Levich lines
shown in (b). These lines are then extrapolated (c) to obtain the electronic transfer current I_t (d).

Performing these three steps at several potential values (Fig. 2a, b, c, d) allows you to plot the Tafel curve (Fig. 2e). The slope of this curve gives the value of the symmetry factor αr while the current value at E = E° gives the value of the standard kinetic constant k°, given the concentration of the reactive species and the number of the electrons involved in the redox reaction.

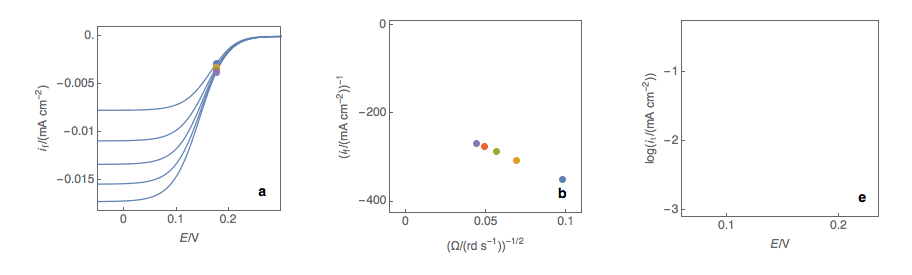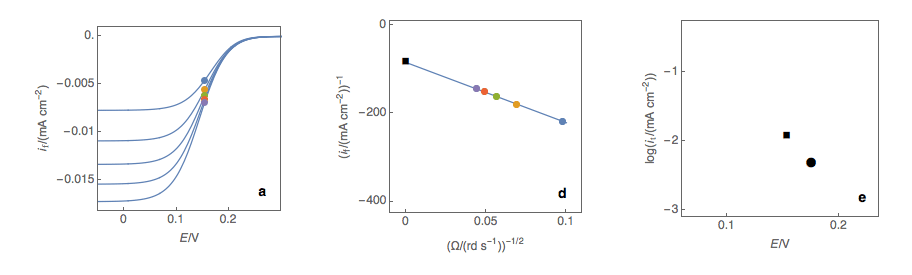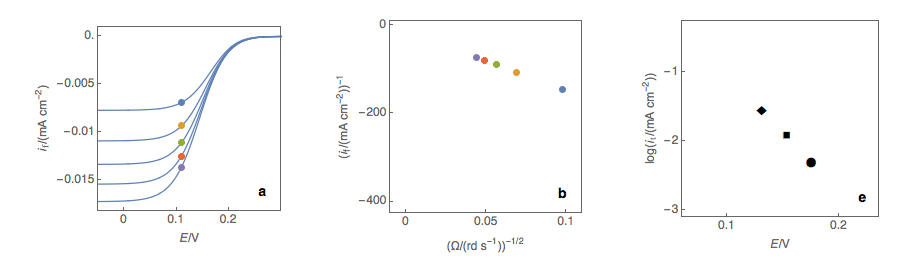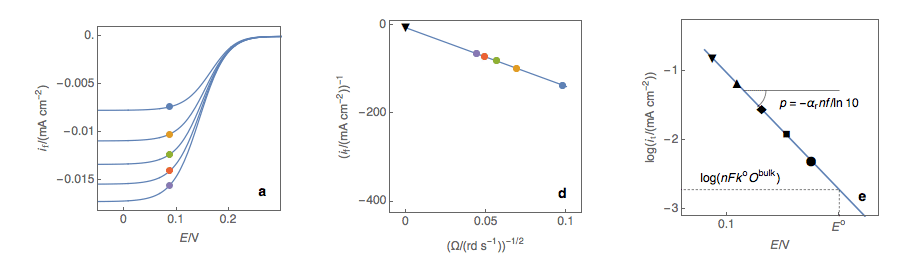
Figure 2: (a) I vs. E curves obtained on an irreversible system on a Rotating Disk Electrode
at various rotation speeds. The dots represent the points chosen to plot the Koutecký-Levich
lines shown in (b). These lines are then extrapolated (c) to obtain the electronic transfer
current I_t (d). This is carried out at various potentials to obtain the Tafel curve shown in (e).

Misusing the Koutecký-Levich analysis to determine the number of electrons involved in the reaction

As mentioned supra the Koutecký-Levich analysis is valid only for sluggish reactions that is to say for k° lower or equal to 10^-2 cm s^-1. In these conditions, the Koutecký-Levich lines are parallel (Fig. 2b) and the extrapolation gives reasonable values (Fig. 2d) for the electronic transfer current I_t(E).

The slopes of the Koutecký-Levich plots could also be used to determine, for example, the number of electrons, based on the concentration and the diffusion coefficient of the reactive species, in exactly the same way it could be done using a Levich plot (Fig. 3a). Again, this is only valid for small values of k° and it would much simpler to use the Levich plot for such a calculation.

As can be seen in Fig. 3c, for k° values that are larger than several 10^-2, the slope of the Koutecký-Levich plots depends on the potential. Using the former expression of the slope would give a number of electrons that depend on the potential, which is not coherent with the hypotheses of the analysis.

For these reasons, please refrain from using the Koutecký-Levich analysis to determine the number of electrons, the Levich analysis is more than enough for that! Both Levich and Koutecký-Levich analyses can be performed in EC-Lab. Please see the corresponding Youtube videos [3,4].

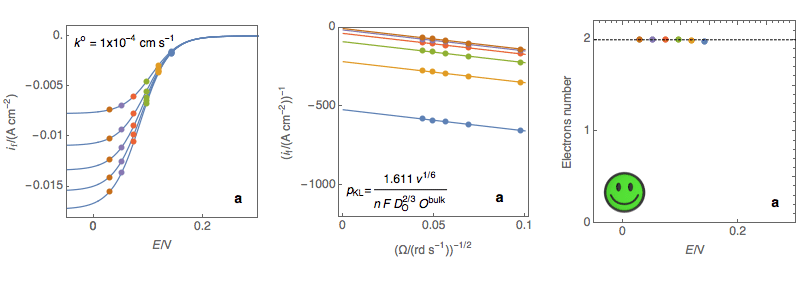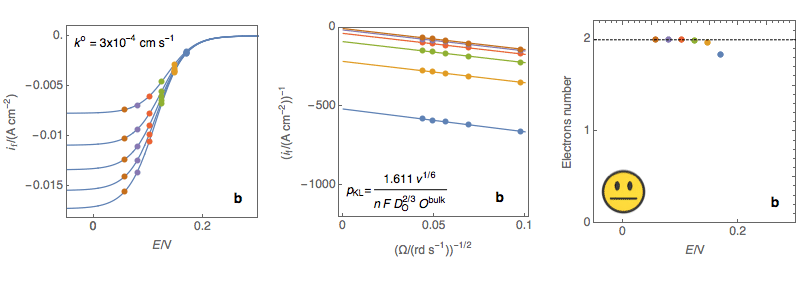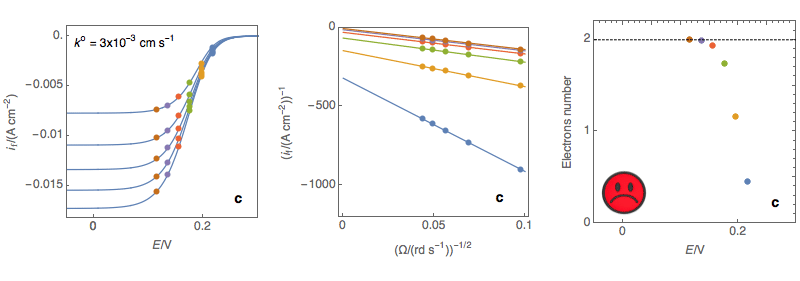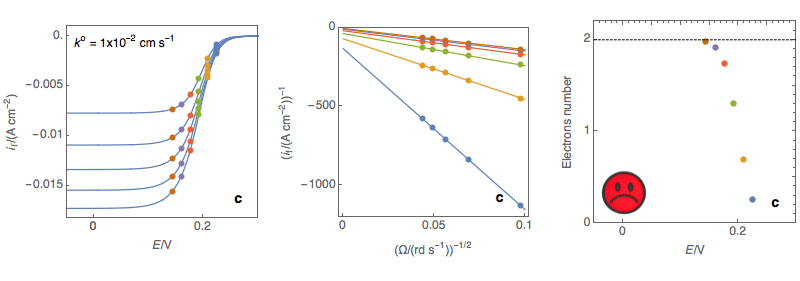
Figure 3: (Left) steady-state I vs. E curves at an RDE for various rotations rates (Center)
Koutecký-Levich plots (Right) Electrons number calculated at each potential using the
expression of the Koutecký-Levich slope for a sluggish reaction (a) Sluggish reaction,
the number of electrons does not depend on potential, OK (b) Neither sluggish nor rapid
reaction, the number of electrons slightly depends on the potential, Acceptable (c)
Rapid reaction, the number of electrons depend on the potential, Not OK