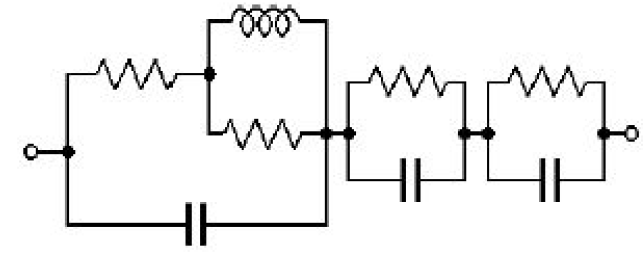
Equivalent model of electrochemical cell inc. ref. electrode impedance and potentiostat parasitics Battery – Application Note 44
Latest updated: May 15, 2024Abstract
As a highly sensitive technique, the electrochemical impedance spectroscopy (EIS) requires basic precautions to obtain reliable results. High impedance cells are more sensitive to capacitive artifacts while the low impedance cells are more sensitive to inductive and resistive artifacts.
Artifacts are even more important as the frequency of analysis now tends to cross the megahertz boundary. Ignoring these artifacts can lead to misinterpretation of the results. In this application note, we focus on the influence of stray capacitances introduced by the instrumentation. We also show that the strange results data obtained with a poor reference electrode can be perfectly explained by a complete model of the cell that includes the instrumental artifacts. Reducing the reference electrode’s impedance can be a straightforward method to minimize instrumentation artifacts coming from the reference electrode. As a general precaution, special care must be taken with the reference electrode to ensure accurate impedance measurements at high frequencies.
EIS Basics
Introduction
As a non-intrusive and highly sensitive technique, electrochemical impedance spectroscopy (EIS) requires basic, often overlooked or ignored precautions, in order to obtain reliable results. High impedance cells are more sensitive to capacitive artifacts while low impedance cells are more sensitive to inductive and resistive artifacts. Artifacts are even more important as the frequency of analysis now tends to cross the megahertz boundary. Ignoring these artifacts can lead to misinterpretation of results. In this note we focus on the influence of stray capacitances introduced by instrumentation. We also show that the strange results obtained with a poor reference electrode data can be perfectly explained by a complete cell model that includes instrument artifacts.
An Analysis Dilemma
Impedance measurement results are analyzed and compared to simulated data generated from mathematical or electrical models. Model parameters are obtained from a data fitting process. Important differences between measured and simulated data can have two causes: either a wrong or incomplete model or an experimental artifact (Fig. 1).
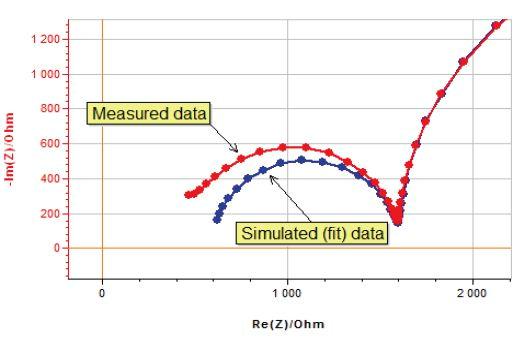
Figure 1 : Analysis dilemma, measured and simulated data do not match.
How do you identify the origin of these differences? Is it a modeling or a measurement problem? Solving this analysis dilemma requires an awareness of possible measurement artifacts.
Table I: True, effective and measured values.
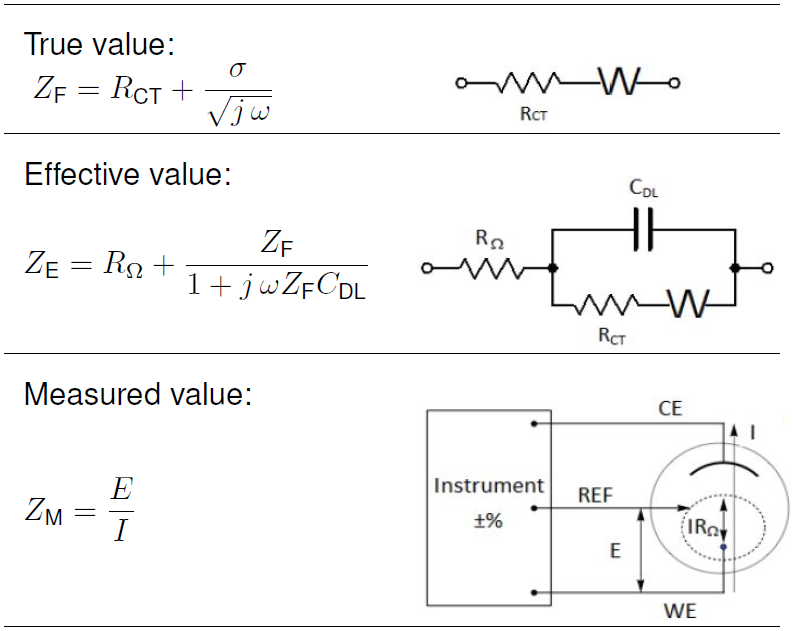
Important differences exist between the true, effective and measured value of an electrochemical impedance. In Tab. I, the true value is the impedance of a basic redox reaction with a semi-infinite diffusion condition. The equivalent electrical model consists of a charge transfer resistance (RCT) in series with a Warburg diffusional element (W). Generally, the true value is the value of interest but it does not take into account parasitics.
The effective value adds to the true value the elements that cannot be avoided in a measurement. In our example, these elements are the double layer capacitance (CDL) and the uncompensated solution resistance (RΩ) related to the electrochemical cell.
The measured or indicated value is the value the instrument displays, hence it reflects its inherent imprecision. A different instrument will show different values. A second measurement will not give the exact same values.
If the quality of the instrument needs to be checked, a dummy cell with a known impedance should be used. Nonetheless, checking the measurement quality of the instrument with a dummy cell is good but not enough.
In typical DC or slow electrochemical measurements with a potentiostat the reference electrode provides a stable voltage reference for the working electrode. However, a reference electrode with a non-zero impedance in combination with the potentiostat’s non infinite input impedance, may play an important role on rapid kinetics analysis or high frequencies impedance measurements. One can either include the reference electrode and potentiostat input impedance in the effective value or, better still, keep them insignificant.
Instrumentation Parasitic
Measurement Method
The measurement principle diagram of the BioLogic SP-200 potentiostat and impedance analyzer is shown in Fig. 2. A sinusoidal signal is generated and applied to the cell over a wide range of frequencies. The working electrode voltage versus the reference is measured by the voltmeter V2. The current is calculated using the voltage V1 measured across the precision resistor Rm.
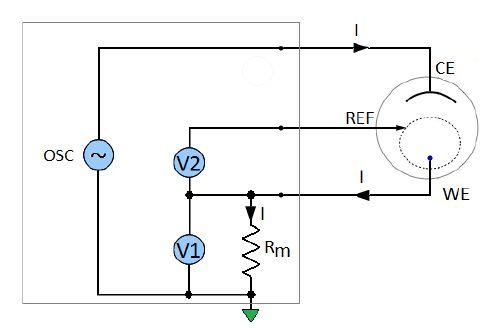
Figure 2: Measurement principle diagram of the Biologic SP-200 potentiostat and impedance analyser.
The unknown impedance of the working electrode is calculated from the measured voltage and current values (Fig. 2):
$$Z_\text{M} = \frac{V_2}{1}=\frac{V_2}{V_1}\, R_\text{m} \tag{1}$$
Potentiostat stray Capacitances
An instrument is made of real, hence imperfect components. At high frequency most of the artifacts come from the input stray capacitances. A model of the instrument is shown in Fig. 3, which includes the main stray capacitances: the counter to the reference capacitance, the reference to the ground capacitance, the reference to the working and the working to the ground capacitance.
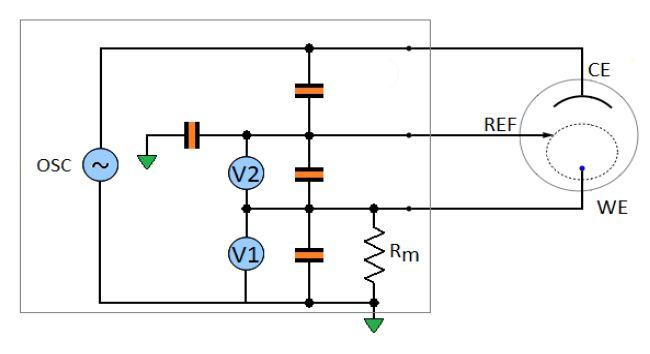
Figure 3: Model of the potentiostat including the four main stray capacitances.
The influence of the stray capacitances of the reference to the working and of the working to the ground are cancelled by the calibration of the instrument at the factory. To calibrate the instrument, standard devices are connected at the end of the leads of the standard cable and the instrument is adjusted (through computation/data storage) so that it measures within the specified accuracy.
EIS Accuracy Plot
In Fig. 4, the shaded areas show different ranges of impedance that can be measured within a specified error in magnitude and in phase. Residual stray capacitances and stray inductances limit the measurement accuracy at high frequencies on high and low impedance cells, respectively. However, this accuracy plot is the highest accuracy one can obtain on standard devices. The electrochemical cell and its environment makes the real accuracy be not as good as the one in this plot. It is important then to understand the origin of the artifacts and to try to minimize them.
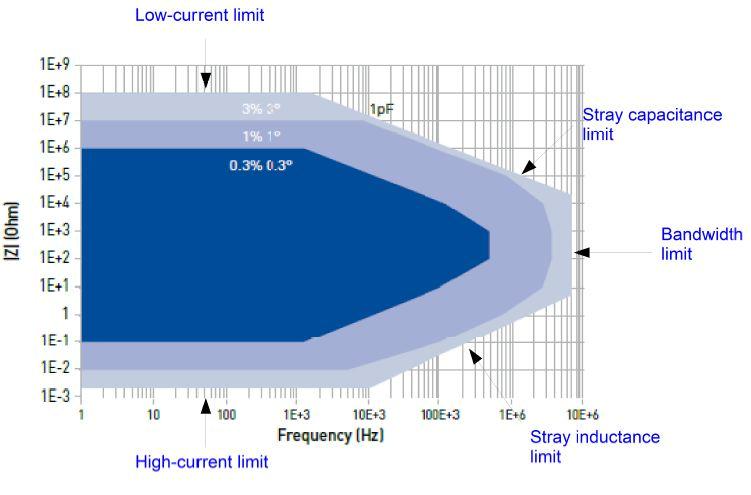
Figure 4: SP-200 contour plot.
EIS On Anelectrical Circuit
For the sake of simplicity, an electrical circuit in the middle range of the potentiostat impedance accuracy plot has been chosen. As expected, the impedance measurement performed with the SP-200 in the high frequency range from 7 MHz to 1 kHz corresponds to the effective impedance of the cell (Fig. 6).
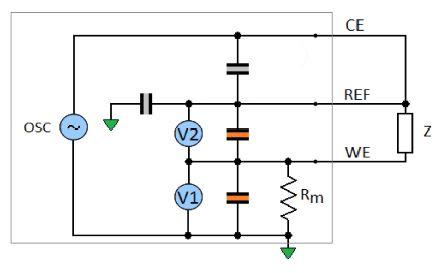
Figure 5: Equivalent model of the potentiostat with simplified artifacts.
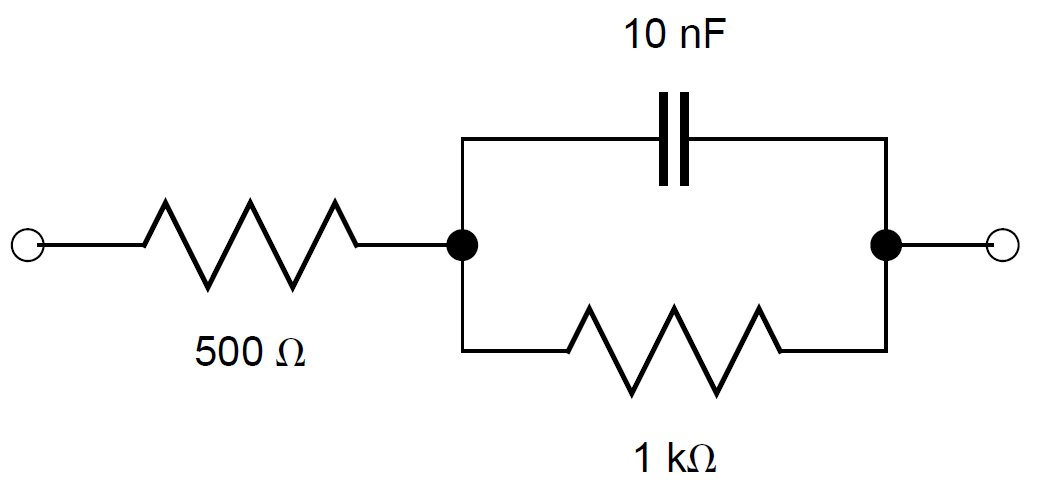
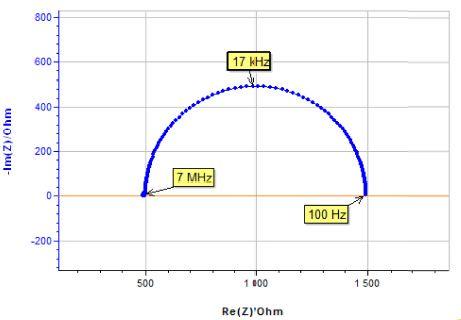
Figure 6: Electrical circuit in the middle range of the potentiostat impedance accuracy plot, corresponding Nyquist impedance diagram.
The same experiment is now performed with a 10 kΩ resistor mimicking a poor reference electrode (Fig. 7).
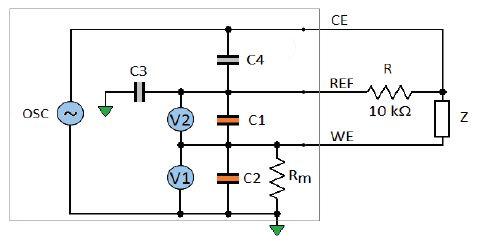
Figure 7: Model of the potentiostat with a simulated poor reference electrode.
The measured impedance (Figs. 6 and 8), represented in red in the Nyquist diagram is far from the previous measurement in blue. The equivalent measured impedance can be obtained from the Kirchhoff’s laws:
It can be noted that if R resistance is zero, the measured impedance Zm equals the effective impedance Z given by (Fig. 6):
$$Z_\text{m}=\frac{Z(1+jωR_\text{m}C_2)(1+jωRC_4)-jωRR_\text{m}C_3}{1+ j \omega R(C_1+C_3+C_4)+j \omega R_\text{m}(C_2+jwRC_1C_3+j \omega RC_2(C_1+C_3+C_4))} \tag{2}$$
With r1 = 500 Ω, r2 = 1 kΩ and c2 = 10 nF.
$$Z = r_1 + \frac{r_2}{1+jωr_2c_2} \tag{3}$$
Figure 8: Measured impedance with poor reference electrode (red dots) and impedance diagram shown in Fig. 6 (blue dots).
Focus On The Reference Electrode
a. Model Fit
The Mathematica software was used to fit the measured data with the equation of Zm (Eq. (1)).The plot obtained using the fit parameters (r1 = 500 Ω, r2 = 1.00 kΩ, c2 = 9.99 nF, R = 10.0 kΩ, C4 = 17.8 pF, Rm = 1.00 kΩ, C1 = 8.56 pF, C2 = 0.344 nF, C3 =52.0 pF), match pretty well the experimental data (Fig. 9). Also, the fit values of stray capacitances of the instrument are in good agreement with the expected values. Thus, we can say that the potentiostat model with artifacts we have proposed is most likely to be the correct one.
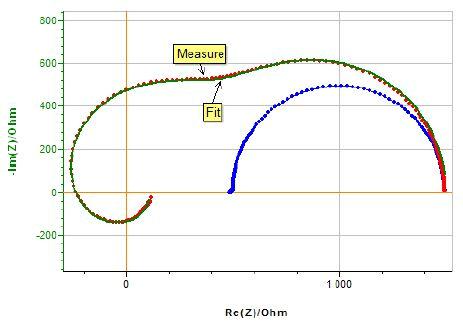
Figure 9: Measured impedance with poor reference electrode (red dots), impedance diagram shown in Fig 6 (blue dots) and fitted curve (green curve).
Generally, a platinum wire and a parallel bypass capacitor should be added to the reference electrode to overcome the EIS high frequency artifacts. BioLogic provides a special EISR-XR820 reference electrode model which includes a bypass 10 nF capacitor. This capacitor makes the reference electrode continue to provide a constant voltage reference while its impedance (reactance) decreases as the frequency increases. Why 10 nF ? The value of this capacitor could be higher but it would not change very much as 1 MHz impedance of a 10 nF capacitor is only 16 Ω. Figure 10 shows the change of Zm with the C4 value. For the sake of simplicity we considered C4 as a reference bypass capacitor. Note that Zm for C4 = 10nF.
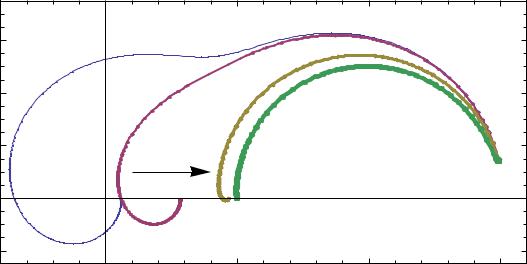
Figure 10: Change of Nyquist diagram of Zm with C4 value. C4/nF = 0:01; 0:1; 1; 10, from left to right.
b. Real electrochemist life
The impedance spectrum (Fig. 11) of a glassy carbon electrode in a ferrocene solution was measured with an R-XR300 Ag/AgCl reference electrode fitted with a bridge tube. An unexperimented user could even find a good fit with a non-realistic equivalent electric circuit.
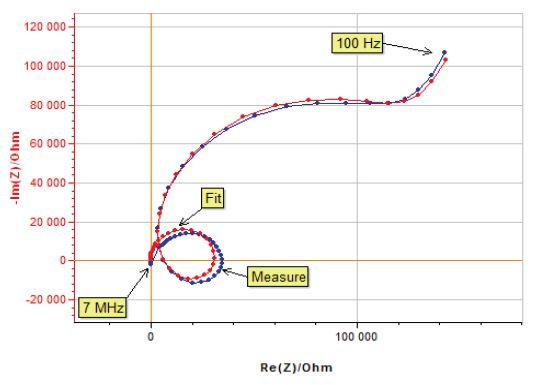
Figure 11: Impedance spectrum of a glassy carbon electrode in a ferrocene solution with a poor reference electrode and fit of the data using the circuit model.
The same experiment was carried out with the R-XR820 AC bypass reference electrode. The two plots move away from each other at relatively low frequency (Fig. 12).
Conclusion
Reducing the reference electrode impedance can be a straightforward method of minimizing instrumentation artifacts originating from the reference electrode. As a general precaution, special care must be taken with the reference electrode to ensure accurate impedance measurements at high frequencies.
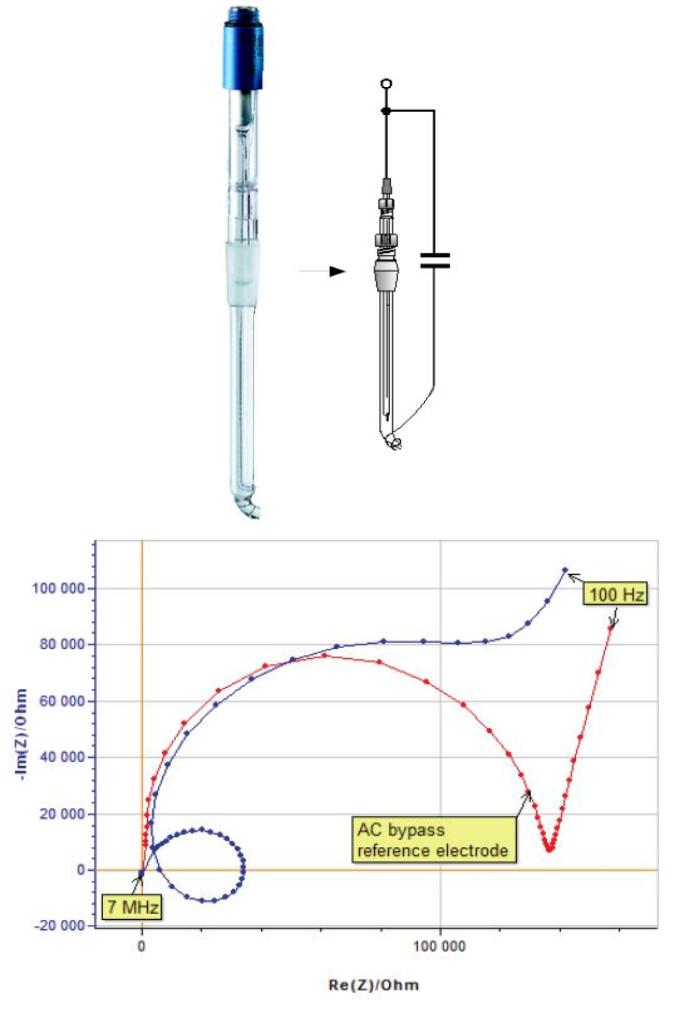
Figure 12: Impedance spectra of a glassy carbon electrode with and without an AC bypass reference electrode (R-XR820).
References
1) Application note #5 “Precautions for good impedance measurements”
2) Keysight Impedance Measurement Handbook. 6thEdition (2016).
3) S. Chechirlian, P. Eichner, M. Keddam, H.Takenouti, H. Mazille, Electrochim. Acta., 35 (1990) 1125.
4) S. Fletcher, Electrochem. Com., 3 (2001)692.
5) A. Sadkowski, J.-P. Diard, Electrochim.Acta., 55 (2010) 1907.
Revised in 01/2020