The mystery of potentiostat stability explained (Potentiostat stability) Battery – Application Note 4
Latest updated: December 19, 2023Abstract
The role of a potentiostat/galvanostat is to apply a desired potential/current and measure the current/potential response in any situation, even in the most difficult operating conditions, for example when the current range increases by 6 orders of magnitude. The bandwidth of the instrument, which is the rate at which the potentiostat can respond to a change in the system, is of critical importance. BioLogic instruments have adjustable bandwidths and this note explains why a potentiostat can start to oscillate in certain conditions and how the choice of the ad hoc bandwidth can eliminate these oscillations.
Introduction
Like the vast majority of research instruments, potentiostats are seldom used in trivial experimental conditions.
Potentiostat/galvanostats do not only have to deal with a vast, highly eclectic range of research activities, but also wide-ranging electrochemical systems and experiments.
Furthermore, due to their nature, the electrochemical experiments evolve over extremely large ranges of values of the significant parameters.
In corrosion applications, for example, recording the current over 5 or 6 current ranges in the same experiment is very common. It is not hard to imagine that, in such a demanding environment, potentiostats are often pushed to their limits and used in situations that may compromise their performance. There are always times when potentiostats do not function as expected. Ringing or oscillations, for example, are signs that a potentiostat is struggling to maintain or has even lost control of the cell’s potential.
This document aims is to clarify the origins of stability problems of such instruments using the example of the VMP3 multichannel potentiostat.
A detailed understanding of what causes instability will increase your confidence, and enable you to experiment with parameters such as “current range” or “bandwidth” or choosing a resistor value in series with the working electrode to settle down your potentiostat without loss of accuracy.
Although we will try to keep the text accessible, a knowledge of potentiostat design and terms like impedance, capacitance, and Bode representation is recommended; as well as basic skills relating to complex number calculus.
Note: VMP3 instrument illustrates this note, but the same specifications can be observed with VMP300, VSP, SP-150, SP-50 potentiostats.
POTENTIOSTAT, BASIC PRINCIPLES
Since 1942, when Hickling built the first three electrode potentiostat, significant progress was made to improve the potentiostat’s capabilities. Hickling had the brilliant idea of automatically controlling the cell potential by means of a third electrode: the reference electrode. This principle remains in practice today.
In its most basic form, a potentiostat measures the potential difference between the working and the reference electrode, applies current through the counter electrode, and measures the current i as an iR drop across a series resistor (Fig. 1).
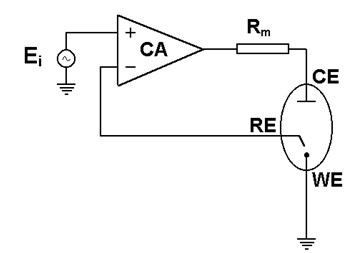
Figure 1: Basic potentiostat design.
The role of the control amplifier (CA) is to keep the voltage between the reference and the working electrode as close as possible to the voltage of the input source Ei. It adjusts its output to automatically control the cell’s current so that this equality condition is satisfied. To understand how it works, we must write down some equations well known by electronics engineers.
Before moving forward with the math, note that from an electrical point of view the electrochemical cell and the current measuring resistor Rm can be considered as two impedances (Fig. 2). Z1 includes Rm in series with the interfacial impedance of the counter electrode and the solution resistance between the counter and the reference electrodes. Z2 represents the interfacial impedance of the working electrode in series with the solution resistance between the working and the reference electrodes.
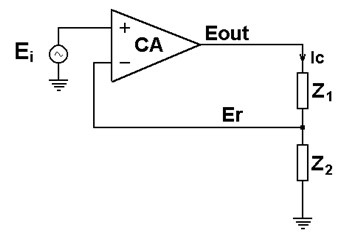
Figure 2: An electrochemical cell and the current measuring resistor can be replaced by 2 impedances.
The role of the control amplifier is to amplify the potential difference between the positive (or non-inverting) input and the negative (or inverting) input. This can be translated mathematically into the following equation:
$$E_\text{out} = A (E^+ – E^-) = A (E_\text i – E_\text r) \tag{1}$$
where A is the amplification factor of the CA.
At this point, we should make the assumption that no or only insignificant current is flowing through the reference electrode. This corresponds to practical examples since the reference electrode is connected to a high impedance electrometer. Thus the cell current can be written in two ways:
$$I_\text C = \frac{E_\text{out}}{Z_1 + Z_2} \tag{2}$$
Or
$$I_\text C = \frac{E_\text r}{Z_2} \tag{3}$$
Combining Eqs. 2 and 3 yields Eq. 4.
$$E_\text r = \frac{Z_{2}}{Z_1 + Z_2} E_\text{out} = \beta E_\text{out} \tag{4}$$
where β is the fraction of the output voltage of the control amplifier returned to its negative input, namely the feedback factor.
$$\beta = \frac{Z_2}{Z_1 + Z_2} \tag5$$
Combining Eqs. 1 and 4 yields Eq. 6.
$$\frac{E_\text r}{E_\text i} = \frac{\beta A}{1+\beta A} \tag{6}$$
When the quantity βA becomes very large with respect to one, Eq. 6 reduces to Eq. 7, which is one of the negative feedback equations.
$$E_\text r = E_\text i \tag{7}$$
Equation 7 proves that the control amplifier works to keep the voltage between the reference and the working electrodes close to the input source voltage.
WHERE ARE THOSE OSCILLATIONS COMING FROM ?
Let’s have a closer look to the control amplifier. Equation 7 is true only when βA is very large. Since the β fraction is always less than one, this means that the amplification factor A must be very large. In practice, the control amplifier amplifies about 1,000,000 times the input difference voltage, but this is true only for low frequency signals. A real control amplifier is made of real, hence imperfect, components and therefore does not amplify in the same way as a low and a high frequency signal. It is natural to think that a slowly varying signal is amplified better than a high-speed signal. The control amplifier is increasingly compromised as the frequency increases because it cannot catch-up with high-speed variation signals. So the amplification decreases as the frequency increases. Furthermore, the output signal is somehow shifted with regard to the input signal. Obviously the amplification is a function of frequency, which can be expressed by a simplified mathematical model described by the complex Equation 8.
$$A(f) = \frac{a}{1+j\frac{f}{f_\text a}} \tag{8}$$
where f is the frequency, a the low frequency amplification, fa is called the break down frequency, and $j^2=-1$.
As for any complex number, the amplitude can be expressed in polar form in terms of magnitude and phase:
$$A = |A|e^{j\varphi A} \tag{9}$$
According to Eq. 8, the magnitude is calculated as:
$$|A|= \frac{a}{\sqrt{1 + \left(\frac{f}{f_a}\right)^2}} \tag{10}$$
and the phase as:
$$\varphi_A = -\mathrm{arctan}\left(\frac{f}{f_\text a}\right) \tag{11}$$
Figure 3 shows the control amplification magnitude and phase plotted vs. frequency for some common values of a and fa. This graphical representation is very intuitive and very close to the real behavior of the control amplifier. The amplification factor goes down for frequencies larger than the break down frequency. When the amplification reaches unity, the control amplifier no longer amplifies; it becomes an attenuator. The frequency at which the amplification reaches unity is called the unity-gain bandwidth.
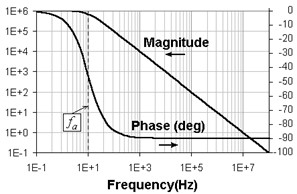
Figure 3: Bode plot of the amplification magnitude and phase for a = 106 and fa= 10 Hz.
Now, let’s go back to Eq. 6 and note that both the fraction β and amplification A are complex numbers. What happens when the quantity βA approaches -1?
$$\beta A = -1 \tag{12}$$
It is not difficult to see that the limit of Eq. 6 is – $\infty$. In this case, the control amplifier output heads to the power supply limit as fast as it can. When the limit is approached, the control amplifier enters a nonlinear zone. At this point, it can either stay forever or head to the other power supply limit and so on until the power supply is disconnected. The second state is named ‘oscillatory’. In both states, the potentiostat has lost the control of the cell, and the system has become unstable. Note that the stability is determined only by the βA factor according to Eq. 12. Thus a stability problem is exclusively due to the control amplifier characteristics, the current measuring resistor (included in Z1), and the cell. It has nothing to do with the excitation signal!
Replacing the polar form of both β and A in the Equation 12 yields Equation 13:
$$|\beta | |A|e^{j(\varphi_{\beta} + \varphi_\text {A})} = -1 \tag{13}$$
which is equivalent to:
$$|\beta | |A|= 1 \tag{14}$$
and:
$$\varphi_{\beta} + \varphi_\text {A} = ±180° \tag{15}$$
We have seen that the phase shift associated with the control amplifier can reach –90° for frequencies over the break frequency (Fig. 3). If phase shift associated with the feedback is important, then the total phase shift may reach –180°. If this occurs at frequencies where Eq. 14 is satisfied, then the system becomes unstable.
A very simple graphical method (also known as the Bode method) can be developed from Eqs. 14 and 15 to determine the stability of a potentiostat. Both ∣A∣ and 1/∣β∣ are plotted as a function of frequency on log-log coordinates as shown in Fig. 3 and Fig. 5. Equation 14 is fulfilled at the interception of the two curves. The total phase shift at the intercept can be determined by relating the phase shift to the slopes of the ∣A∣ and 1/∣β∣ curves. As shown in Fig. 3, the magnitude rolls-off with a factor 10 within one decade of frequencies and the phase shift reaches –90° for frequencies over the break frequency. Generally a negative magnitude slope of -10/decade corresponds to –90° phase shift while a positive 10/decade to +90° phase shift. Thus, if at the intercept point the ∣A∣ slope falls with -10/decade and the 1/∣β∣ slope rises with +10/decade, then the total phase shift expressed by the Eq. 15 approaches 180° and the potentiostat is unstable.
PRACTICAL SITUATIONS
Connecting a highly capacitive cell to a potentiostat can be a troublesome experience especially when the application requires a sensitive current range. Generally things become worse in more sensitive current ranges. The reason is that this type of cell, along with the current measuring resistor, introduces important phase shifts in the feedback signal.
Let’s take a simple cell equivalent circuit for a nonfaradaic system (Figure 4).
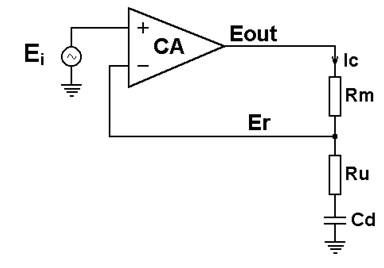
Figure 4: Dummy cell for a nonfaradaic system.
In this equivalent circuit, the uncompensated solution resistance between the reference and the working electrodes is represented by the resistor Ru, Cd is the double-layer capacitance of the working electrode, and Rm is the current measuring resistor. The impedance of the counter electrode and the solution resistance between the counter and the reference electrodes have been neglected for the sake of simplicity (these impedances can be added to the series with Rm for a more sophisticated analysis). In the circuit shown in Figure 4, the previously defined Z1 and Z2 impedances are expressed by Eqs. 16 and 17.
$$Z_1 = R_\text m \tag{16}$$
$$Z_2 = R_\text u + \frac{1}{j2\pi fC_\text d} \tag{17}$$
Replacing terms in Eq. 5 yields the feedback factor:
$$\beta = \frac{1+j\frac{f}{f_2}}{1+j\frac{f}{f_1}} \tag{18}$$
where
$$f_1 = \frac{1}{2\pi (R_\text m + R_\text u)C_\text d} \tag{19}$$
and
$$f_2 = \frac{1}{2\pi R_\text uC_\text d} \tag{20}$$
Now let’s perform the stability analysis by the Bode method, for some particular values of the dummy cell circuit (Figure 5). The amplification magnitude ∣A∣ corresponds to the VMP3 control amplifier with the bandwidth factor set to 5. The 1/∣β∣ quantity is calculated for Cd= 1 µF, Rm= 100 kΩ (10 µA current range), Ru= 1 kΩ (curve “b”), and Ru= 0 Ω (curve “a”). The frequencies f1 and f2 defined by the Equations 19 and 20 correspond to the 1/∣β∣ break frequencies.
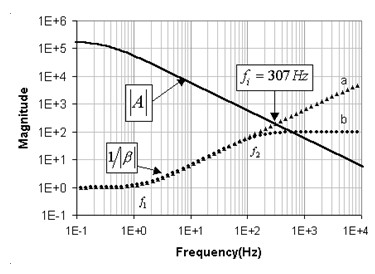
Figure 5: Bode plots for Figure 4 dummy cell. Cd= 1 µF, Rm= 100 kΩ, Ru= 1 kΩ (b), Ru = 0 Ω (a).
According to the Bode method, the phase shift can be correlated to the slope of the ∣A∣ and 1/∣β∣ curves at the critical interception point. When Ru is set to zero, the 1/∣β∣ “a” curve has a slope of 10 by one decade of frequency and the ∣A∣ curve has a –10/decade slope for about –180° total feedback phase shift at the interception point frequency (307 Hz). This situation will cause oscillations. When the Ru= 1 kΩ, the intercept point moves to a higher frequency where the 1/∣β∣ “b” curve has a slope very close to zero. Under these circumstances, the oscillation condition is not met and the system should be stable.
This stability analysis is in perfect agreement with the true behavior of the VMP3 connected to this type of cell. Figure 6 shows a voltage step response of the system recorded with the EC-Lab® software. Counter, counter sense, and reference leads were stuck-together (CA1, REF3 and REF2) as well as the working current with the sense lead (CA2 and REF1). In this test, the cell potential and current are recorded on the 10 µA current range following a 100 mV voltage step.
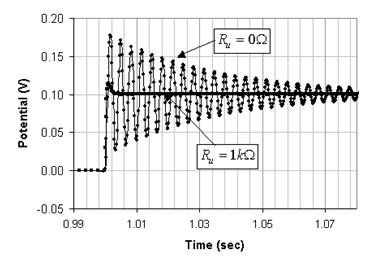
Figure 6: Step response of the VMP3 for the Figure 5 dummy cell values.
Figure 5 predicts a stable state when Ru= 1 kΩ. Indeed, Figure 6 shows that the cell potential quickly reaches the 100 mV level with a small overshoot following the voltage step made at 1.0 seconds.
Conversely, when Ru is set to zero, the system oscillates as expected. Although, the oscillation does not last forever. The oscillation amplitude is attenuated in time, and the system finally converges to the 100 mV voltage level. Accurate calculation at the intercept point shows that the phase shift misses about 0.7° from the “perfect” –180° oscillation condition. It is interesting to note that the frequency of the oscillation matches the intercept point frequency. One can count about 6 periods in 20 ms, which yields an oscillation period of 3.3 ms thus a frequency of 300 Hz.
To summarize, potentiostats generally provide different iR compensation techniques to reduce Ru solution resistance. Normally the iR compensation cannot completely remove the uncompensated resistance and often leads to instability problems. This behavior can now be perfectly understood by the stability analysis prescribed in this note.
THE BANDWIDTH PARAMETER
To adapt to most practical situations, the VMP3 was designed with the ability to change the control amplifier bandwidth. By changing the bandwidth, one can “move” the system from an unstable state to a stable one. Seven stability factors (also called compensation poles) are proposed which correspond to the same number of bandwidths of the control amplifier. As a reference, the highest value (7) corresponds to the highest bandwidth of 680 kHz and the lowest (1) to the lowest bandwidth of 32 Hz. Intermediate values are shown Table 1.
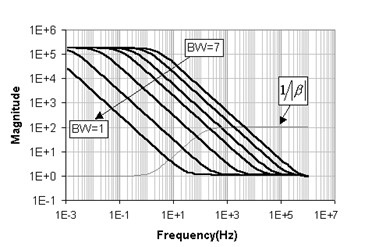
Figure 7: VMP2 control amplifier bandwidths.
Generally, the narrower the bandwidth (i.e. the lower the value), the more stable it gets, but this is not compulsory as shown in Figure 7. Sometimes the system may become stable when the bandwidth is increased, so if decreasing does not render the potentiostat stable, try to increase it.
Figure 7 shows, along with the VMP3 gain magnitude for the different bandwidth factors, the quantity for the previously defined dummy cell. As can be quickly seen, the system should be stable with the bandwidths factors 7, 6, and 5; it will probably manifest an important overshoot with 4 and go into strong ringing or even oscillations for 3, 2, and 1.
STABILITY CRITERION FOR A CAPACITIVE CELL
A straightforward stability criterion can be deduced when the cell is a simple capacitance:
$$f_\text {BW} < \frac{I_\text {max}}{4\pi C} \tag{21}$$
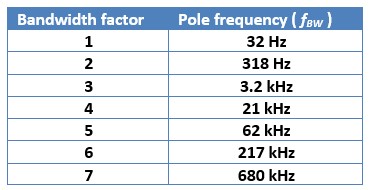
where fBW is the unity-gain bandwidth in Hz (Tab. I), C is the capacitance in F, and Imax is the maximum current of a current range in A.
Table I : Bandwidth poles
Equation 21 yields to a simple abacus shown in Figure 8. To find the bandwidth factor for a stable system, locate the intercept point of the capacitance with the desired current range. All the bandwidths on the right side of this point will provide stability.
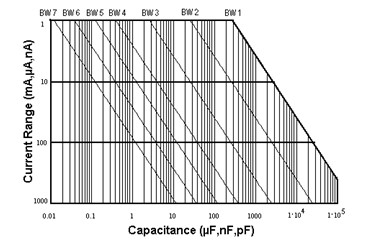
Figure 8: VMP3 stability abacus; current range vs. capacitance: mA/µF, µA/nF, nA/pF.
1. C= 1 nF, Imax= 10 µA the stability can be acquired for BW5 – BW1
2. C= 1 µF (1000 nF), Imax= 100 µA the stability can be acquired for BW2 – BW1
3. C= 10 µF (10000 nF), Imax= 10 µA the stability cannot be acquired
If the stability cannot be acquired with one of the bandwidth factors, a resistor should be added in series with the capacitance. A series resistor will have the same effect as the uncompensated solution resistance: it will stabilize the system but it will introduce an iR drop error. The resistor should have a minimum potential drop across it in order to have minimum influence on the working electrode potential. A good compromise is to admit a maximum iR drop of 1 mV.
The minimum resistor in series with a capacitance for a given current range and a given bandwidth factor is given by Equation 22.
$$R_\text {min} = \sqrt{\frac{2}{\pi f_\text {BW} I_\text {max} C}} \tag{22}$$
As an example, for C = 1000 µF, Imax = 10 µA, and bandwidth 7 (fBW = 680 kHz), the stabilizing resistor would be about 10 W.
Note that higher the bandwidth the smaller the series resistor value, thus the smaller the iR drop error.
STABILIZING THE POTENTIOSTAT
If the potentiostat is showing signs of instability, it is important to note that this may be due, in part, to the cell.
After all, the cell is part of the feedback element of the control amplifier. The most effective way of find out out what is happening, is to draw a circuit model of the cell, compute the feedback factor β, and use the Bode method for the stability analysis.
This may prove a difficult task since the electrochemical cells are seldom made of just simple capacitors and resistors.
If you want a quick solution to your problem without going into detailed stability analysis, you may follow these steps:
- Check your reference electrode. Make sure that the inside solution of the reference electrode has good contact with the bulk electrolyte of the cell. If the porous junction is not wet, then the electrode may have enormous impedance and together with the electrometer input capacitance may introduce a supplementary phase shift on the feedback.
- Change the Bandwidth factor. Start with a lower value. If decreasing does not work, try to increase it.
- Choose a higher current range. Since the current measuring resistor is part of the feedback, the lower it is, the more stable the system gets. But there is a limit on how small a measuring resistor can be. If it is too small, you will not be able to detect the low currents.
- If after the previous steps, the system is still unstable, then you have to think about adding a resistor in series with the working electrode. When the cell is highly capacitive and you have an idea about the double layer capacitance, then use Eq. 22 to determine the resistor value.
- Reduce, if possible, the surface of the working electrode. Since the double layer capacitance is proportional to the electrode area, lowering the surface will reduce the capacitance, which is generally responsible for the instabilities.
- Reduce also, if possible, the impedance between the counter and the reference electrode. This includes the interfacial impedance of the counter electrode and the solution resistance between the two electrodes.
Conclusion
Potentiostats are very powerful instruments with many applications, but we have to be careful: we have demonstrated in this application note how the potentiostat can lose control of the cell. By understanding the mechanism of a potentiostat, and why it sometimes loses control, the user will be more able to avoid such problems.
References
- R.R. Schroeder, I. Shain, Chemical Instrumentation, 1(3), (1969) 233.
- A.J. Bard, L.R. Faulkner, in: Electrochemical Methods Fundamentals and Applications, (2001).
- J.G. Graeme, in: Burr Brown Applications Handbook, (1994) 194.
- R. Mancini, Op Amps For Everyone, Texas Instruments, SLOD006B.
Revised in 07/2018