Internal Resistance series. Part I: What is internal resistance in a battery?
Latest updated: November 15, 2024Part I: What is internal resistance in a battery?
Introduction
The field of battery and energy storage continues to grow exponentially with the development of consumer electronics and electric vehicles, among other key technologies, As a result, laboratories and industry are constantly looking to find new ways of improving battery performance and gaining competitive advantage, notably via reliability and longer battery life. They also need to understand and quantify battery degradation during its cycle life. One of the key parameters affecting those challenges is battery internal resistance. This series of 3 articles will help you to understand what internal resistance is and how it can be measured.
Batteries cannot be considered to be perfect devices, and neither are they pure voltage sources. One of the imperfections of the battery is the voltage drop and the loss of electromotive force $emf$ that occurs when we start drawing current from the battery.
This loss can be characterized by a quantity called internal apparent resistance ($R_\mathrm{int}$) in $\Omega$ or apparent resistance ($\mathrm{R_{app}}$). Internal apparent resistance is a generic term that does not refer to any specific resistance in the battery. In practical terms, it is a generic term that refers to the battery’s natural predisposition to hinder current flow.
Figure 1 shows the evolution of the battery voltage $U$ as it delivers a current $I_0$ with $I_0>0$. Its voltage is instantly decreased by a value $R_\mathrm{\Omega}I_0$ (see the ohmic resistance definition below) and then by a value $R_\mathrm{int}I_0$ that varies with time.

Figure 1: Battery electrode voltage $U$ as a function of time when it delivers a current $I_0$. $E$ represents the batterie $emf$.
The International Electrotechnical Commission (IEC) gives the following definition of internal apparent resistance: Quotient of change of the voltage of a battery by the corresponding change in discharge current under specified conditions.
To introduce the effects of internal resistance on the battery, we can draw an analogy with two ski races. In Figure 2, two skiers simultaneously descend a slope. On the left (Fig. 2a.), a downhill skier heads straight down while, on the right (Fig. 2b.), a mogul skier will encounter some obstacles/bumps and therefore cannot go as fast as the downhill skier.

Figure 2: Internal resistance skier analogy: a) the downhill skier; b) the mogul skier.
The analogy of electrochemistry and battery cycling relates to the following:
- The skier’s speed corresponds to the current that passes through the system, with $I_1<I_2$.
- The height difference can then be compared to the voltage $U$ that decreases during this action.
- The bumps represent the internal resistance $R_\mathrm{int}$.
The more bumps there are, the more difficult it will be for the skier to gain speed! We can extend this analogy to batteries: the ability to deliver a high current or power can be reduced because of internal resistance.
Which phenomena contribute to internal resistance?
Internal resistance can be described as a dipole that follows Ohm’s law and that is an approximative combination of the ohmic drop resistance of all the components of the battery, the charge transfer resistance, and the diffusion resistance of the battery’s electrodes.
A battery can be represented, as shown in Figure 2, as an electromotive force, $E$, in series with a resistor $R_\mathrm{int}$ i.e., the internal apparent resistance.

Figure 3: Simplified electrical model of a battery.
Please note: the “perfect” battery would be represented without the resistance $R_\mathrm{int}$.
Throughout the lifespan of the battery, the internal resistance increases because of the aging of components, electrolyte, etc.
What are the differences between internal resistance and ohmic resistance?
Ohmic resistance, $R_\Omega$, also referred to as high-frequency resistance, $R_\mathrm{HF}$, is defined by the electric resistance of electronic and ionic conductor materials such as connectors, contacts, electrodes, electrolytes, etc. It is also represented by a dipole that follows Ohm’s law.
Internal resistance is a more general quantity including phenomena relevant to ohmic resistance.
What are the consequences of internal resistance on the battery?
Internal resistance can have a significant impact on the battery’s performance, durability, and safety.
As already shown in Figure 1, the most direct effect of internal resistance on batteries when a current flows, is the voltage drop due to the presence of this resistance. Figure 4 shows a battery in a circuit with a resistance $R$, delivering a current $I=V/R$ with $I>0$ and where $V$ is the voltage at the resistance terminals, which is equal to the voltage at the battery terminals (Fig. 4).
As established previously, $R_\mathrm{int}$ can be approximated by a dipole that follows Ohm’s law.
$V=E – R_\mathrm{int} I $
Thus, the battery voltage drop due to internal resistance is $IR_\mathrm{int}$.
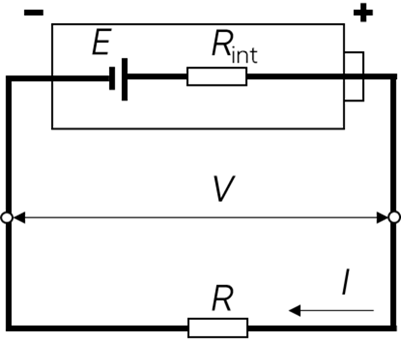
Figure 4: Circuit with a battery discharging in a resistance $\pmb{R}$.
Note that if the circuit is opened, using a switch, no current flows through the circuit so the battery does not experience any voltage drop.
The effect of internal resistance can differ from one battery chemistry to the other. Using the example of the lithium-ion battery, an increase in internal resistance results in a loss of lithium inventory, which in turn, reduces the battery’s capacity.
Internal resistance is also a safety issue. Indeed, according to the Joule effect, the fact that the battery hinders the current’s passage will generate thermal heating. If the temperature becomes too high, it will eventually lead to a thermal runaway and be harmful to the system and everything around it.
To learn more about how to measure internal resistance, please visit the 2nd article in this series: “How to determine the internal resistance of a battery”
For more specific information about Alternating and Direct Current Internal Resistance techniques (ACIR and DCIR), please see the 3rd article in the series.
References
[1] Quantities, Units and Symbols in Physical Chemistry, International Unions of Pure and Applied Chemistry (IUPAC) Commission on physicochemical symbols, terminology and units, 2nd Edition, Blackwell Science Ltd Eds., Oxford (1993).





