What is a Frequency Response Analyzer (FRA)?

Impedance studies (see https://biologic.net/topics/what-is-eis/) offer a deeper understanding of electrochemical systems. But the study of alternative signals leads to technological challenges that impedance analyzers, and more generally, Frequency Response Analyzers (FRA) will encounter.

What is a Frequency Response Analyzer?

As the name suggests, an FRA analyzes the output signal of a stimulated system. It is based on the Fourier Transform analysis (see description below) that allows the study of the signal in the frequency domain rather than in the time domain to characterize the system under test.

What is the principle of the Fourier Transform analysis?

The Fourier Transform analysis is based on the statement that all periodic signals can be broken down into a sum of several sinusoidal signals? Figure 1 describes the example of the triangle wave.

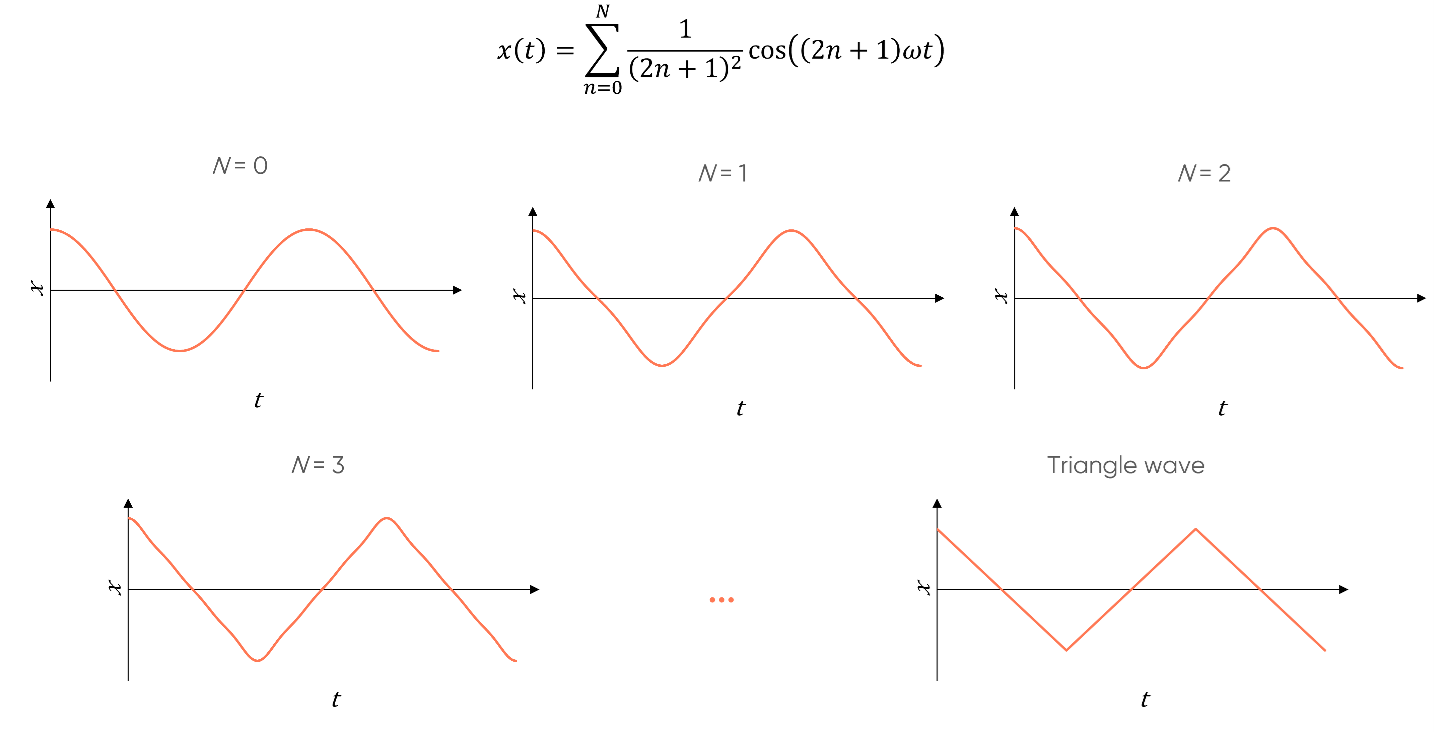
Figure 1: Example of an expression leading to a triangle wave by the addition of sinusoidal components.

Figure 2 describes the example of the square wave.

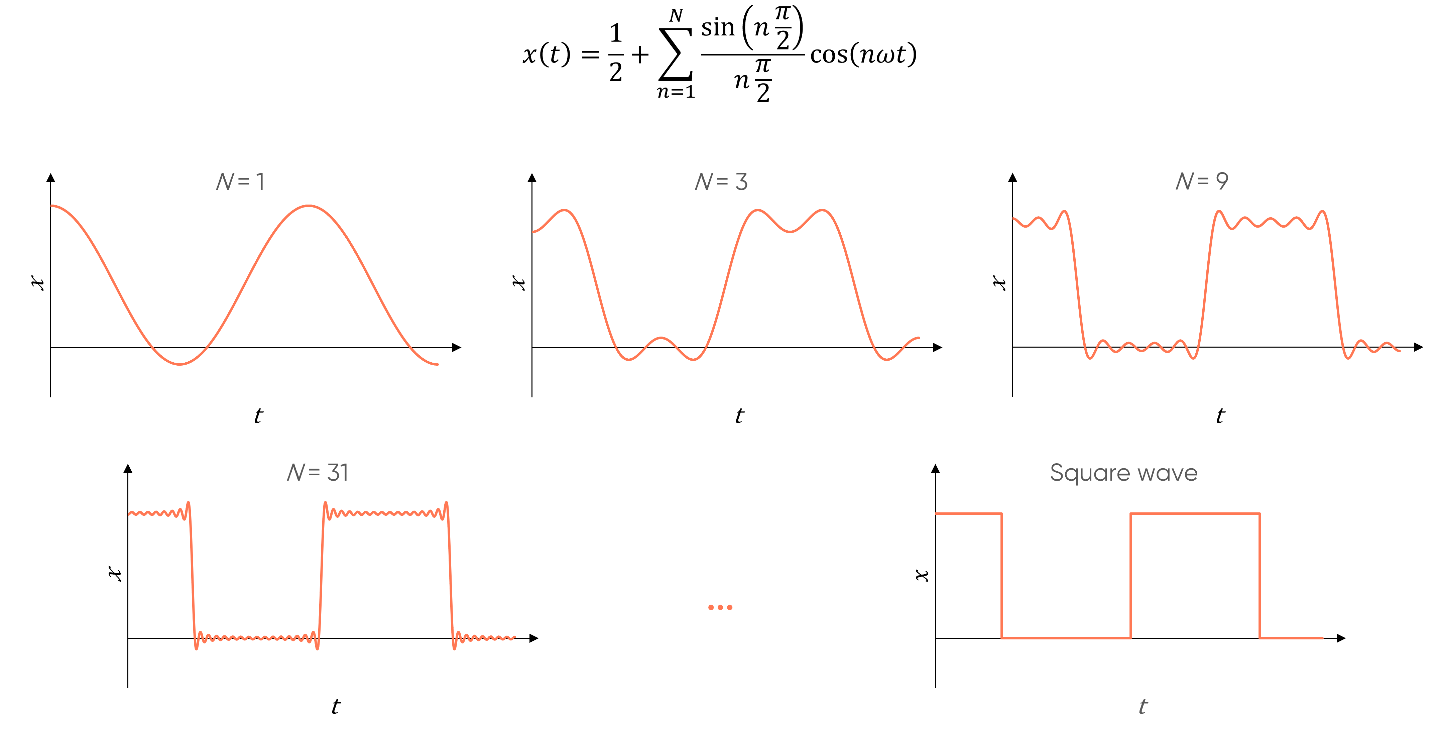
Figure 2: Example of an expression leading to a square wave by the addition of sinusoidal components. 

The expressions above stem from the Fourier series:
$$x(t)=a_0+\sum_{n=1}^\infty\left(a_n cos\frac{2 n \pi t}{T}+b_n sin\frac{2 n \pi t}{T}\right)$$

$a_n$ and $b_n$ are Fourier coefficients.

The Fourier transform allows studying signals in the frequency domain rather than in the time domain. It breaks down the signal into several sinusoidal signals and plots the amplitude of each signal versus frequency. An example is given in Figure 3.

The expression of the signal of Figure 2 for $N=1$ is: $x(t)=cos(\omega t)+\frac{1}{9}cos(3\omega t)=x_1(t)+x_2(t)$.

With ${\omega}/{rad.s^{-1}}=$ pulsation of the signal $ =\frac{2\pi}{T}$

$T/s=$ period of the signal $x(t)$

It is the sum of $x_1(t)$ and $x_2(t)$ where:

$x_1(t)=cos(\omega t)$ à Amplitude of the signal $x_1(t)=1$ and frequency of the signal $x_1(t)= \frac{\omega}{2\pi}=\frac 1T$.

$x_2(t)=\frac{1}{9}cos(3\omega t)$ à Amplitude of the signal $x_2(t)=\frac{1}{9}$ and frequency of the signal $x_2(t)= 3\frac{\omega}{2\pi}=\frac 3T$.

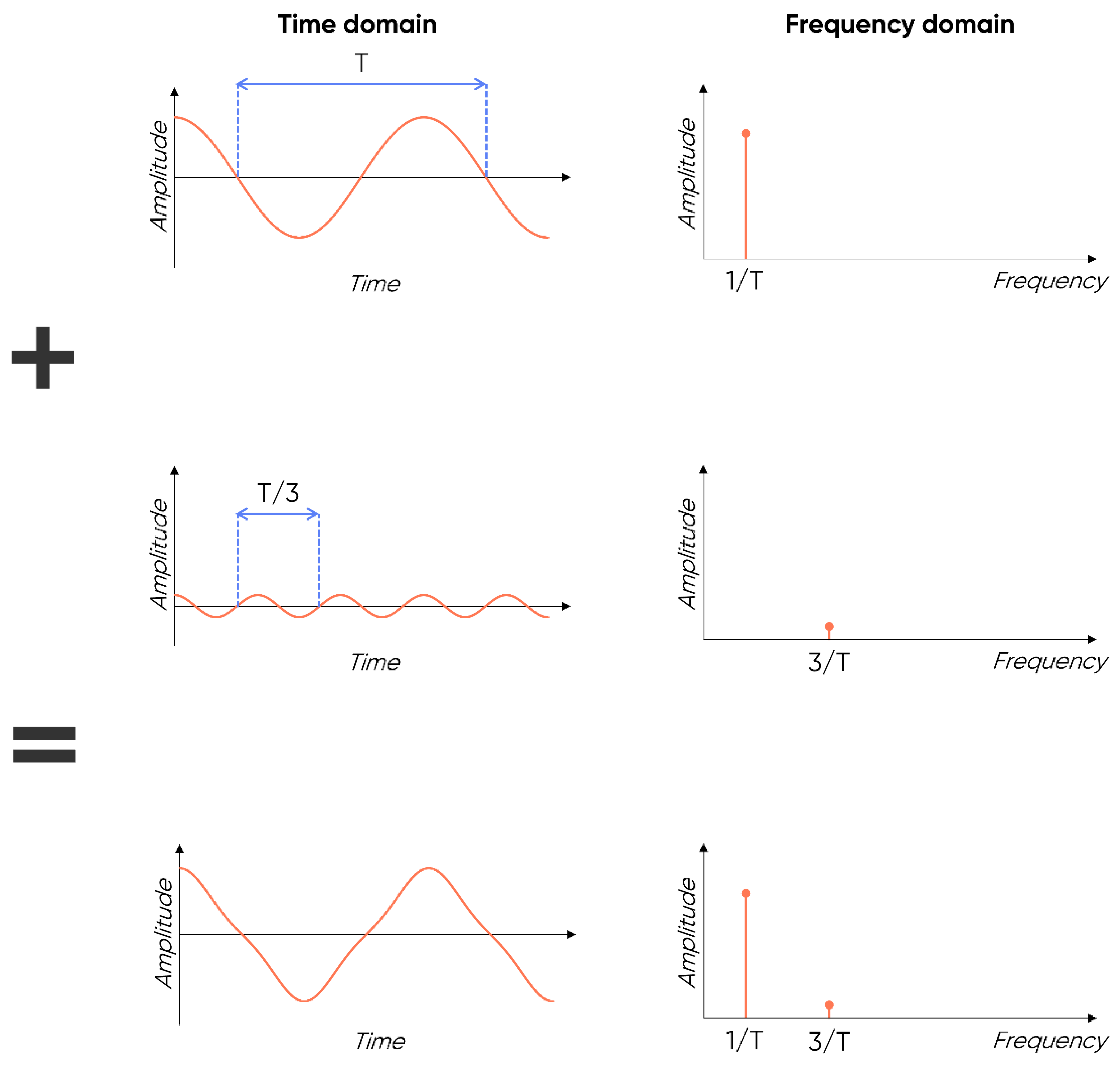
Figure 3: Example of Fourier Transform.

The graphs described in the “frequency domain” are the Fourier transforms of the signals shown in the time domain.

How does a FRA system work?

The FRA system applies the perturbating signal $X(t)$ to the device under test and analyses the device response $S(t)$ by multiplying and integrating the signal as shown in Figure 4 below. The FRA system is able to analyze a periodic signal, no matter the nature of the signal. It can be current or potential signals for electrochemical experiments, but it can also be mass variation for gravimetric experiments for example.

Figure 4: Principle of FRA system. 

In electrochemistry, FRA is associated with the potentiostat that provides input DC current or potential signal. Figure 5 below describes the general principle of such a system.

Figure 5: Principle of an FRA system associated with a potentiostat / galvanostat 

$X(t)$ is a sinusoidal signal generated by the FRA system and sent to the potentiostat.

Voltage and current signals are multiplied by both sine and cosine of the test frequency. The results of the multiplications are integrated over a period T that has to be an integer multiple of the test frequency.

For more detailed information concerning the functioning of the potentiostat itself, visit the article https://biologic.net/topics/what-is-a-potentiostat-how-potentiostats-work-and-their-use-in-science-and-industry/.

The output data of the analyzer are the imaginary and real parts of the current and the voltage. These data allows the calculation of the impedance of the system.

$$Z(\omega)=\frac{Re\;E+j\,Im\;E}{Re\;I+j\,Im\;I}$$

The FRA system is integrated into Biologic’s potentiostats / galvanostats.

What is the difference between an impedance analyzer and a Frequency Response Analyzer (FRA)?

An impedance analyzer is only able to study voltage and current signals in the frequency domain while an FRA can study any signals without distinguishing the nature signals.